PokMovies votre gestionnaire de films et séries
Connectez-vous pour ajouter des films et séries à votre liste personnelle
Voyages au pays des maths (2021) - TV Series Streaming, distribution et critiques
Détails pour Voyages au pays des maths

Voyages au pays des maths (2021)
Voyages au pays des maths (2021)
C’est un pays exotique et déroutant que celui des maths. On y parle une langue bizarre, pleine d’homéomorphismes, de variétés différentielles, de nombres transfinis… Mais on y trouve aussi des paysages épiques, des idées vertigineuses et même, parfois, des choses utiles ! Cette websérie animée propose à tous les curieux munis d’un cerveau en état de marche une visite inédite au pays des maths. Avec un guide, bien sûr !
Date de sortie :
Durée : 10 min/épisode
Statut : En cours de diffusion
Genres : Documentaire
Pourquoi Regarder Voyages au pays des maths ?
Acclamé par la critique avec une note de 8.5/10, Voyages au pays des maths offre une expérience documentaire exceptionnelle à travers 2 saisons captivantes. Un favori éprouvé parmi les amateurs de Documentaire.
Faits Rapides sur Voyages au pays des maths
- Titre : Voyages au pays des maths
- Année de Sortie : 2021
- Type : Série TV
- Note : 8.5/10 (2 votes)
- Genres : Documentaire
Découvrir Voyages au pays des maths en Streaming
Vous cherchez où regarder Voyages au pays des maths en ligne ? Vous êtes au bon endroit ! Sur PokMovies, vous trouverez toutes les informations sur Voyages au pays des maths en streaming, y compris où le regarder légalement, le casting complet, les avis des utilisateurs et la bande-annonce officielle.
Sorti en 2021, Voyages au pays des maths appartient aux genres Documentaire et a reçu une note de 8.5/10 sur The Movie Database avec 2 votes d'utilisateurs.
Cette série TV, actuellement en cours de diffusion, compte 2 saisons. Avec des épisodes d'environ 10 minutes, Voyages au pays des maths vous offre une expérience de visionnage qui est exceptionnelle et a conquis de nombreux fans de séries.
Saisons et Épisodes
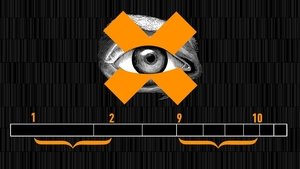
La Loi de Benford
Tout commence comme un étrange complot : le 1 est surreprésenté dans la population des nombres ! C’est vrai sur les étiquettes de la supérette en bas de chez moi ; c’est vrai aussi au fin fond de l’Univers. Cette bizarrerie statistique nous aide à comprendre deux visions du monde complémentaires : la première est linéaire, la seconde logarithmique.

Flâneries infinitésimales
Longtemps les mathématiques ont été une science statique, un temple grec aux proportions parfaites. Il y était question de régularités et de constantes. Puis, avec Newton et Leibniz, le mouvement s’est glissé sournoisement dans le tableau grâce à une invention qui a fait entrer le changement dans le champ des mathématiques : le calcul infinitésimal.
La Conjecture de Poincaré
En 2006, Grigori Perelman est venu à bout de la conjecture de Poincaré, un problème alors ouvert depuis plus d’un siècle et dont la résolution était mise à prix : un million de dollars ! Qu’est-ce qui se cache derrière ce « problème du millénaire » ? Pour le comprendre il faut passer par des sphères plates et des carrés sans bord.

Sur la route de l’infini
En route pour une petite balade à la découverte d’un monde gigantesque ! On y trouvera des nombres auprès desquels le milliard fait figure de miette et on y apprendra à mesurer les infinis. Et je dis bien LES infinis puisqu’on sait depuis Georg Cantor (1845/1918) que l’infini existe en plusieurs tailles.

Le Théorème de Gödel
Les maths, on le sait, sont le domaine de la certitude : soit c’est démontrable, soit c’est faux. Sauf que c’est précisément l’inverse qu’a prouvé le théorème de Gödel : au sein de tout système formel suffisamment complexe pour englober l’arithmétique, il existe des propositions « indécidables », qu’on ne peut ni prouver ni réfuter !

Le Dilemme du prisonnier
Ambiance polar. Un braquage a mal tourné : vous et votre complice êtes interrogés par la police et il faut faire un choix : trahir votre partenaire, ou vous en tenir au silence. Dans cette situation stressante, l’option optimale n’est bizarrement pas la meilleure des options. Heureusement, John Nash et la théorie des jeux sont là pour vous guider.

Sur les traces du jeu de la vie
Inventé par un mathématicien américain (John Horton Conway) dans les années 60, le jeu de la vie est un « automate cellulaire » particulièrement visuel qui permet de mieux comprendre « l’émergence », c’est-à-dire la façon dont un système complexe peut émerger de quelque chose de plus simple. Une histoire qui – soit dit en passant – rappelle un peu celle de notre Univers.

Les Nombres irrationnels
Les nombres irrationnels sont connus depuis au moins 25 siècles, il serait temps de s’y mettre ! Tout ça remonte à Pythagore (−580/−495) et à cette diagonale dont le carré est égal à la somme des carrés des côtés… C’est à cause de cette diagonale que le monde bien ordonné des entiers naturels et des fractions va devoir s’élargir pour accueillir des monstres comme π et √2.

Pique-nique sur le plan complexe
Depuis Jérôme Cardan, fameux astrologue italien du XVIe siècle, on sait que certaines équations semblent admettre pour solutions des nombres… qui n’existent pas ! C’est évidemment embêtant… Mais cet inconvénient aboutira quelques siècles plus tard à la découverte d’un nouveau domaine des nombres : les « complexes », dont ni les mathématiques ni la physique ne peuvent plus se passer.

Cap sur l'hypothèse de Riemann
Fin des voyages au pays des maths avec une randonnée ardue. Mieux vaut avoir bien pris des forces sur le plan complexe. Car il s'agit d'un mystère non-résolu des mathématiques, à savoir : la répartition des nombres premiers. Choisie par David Hilbert en 1900 comme l’une des questions mathématiques les plus importantes du siècle à venir, l’hypothèse de Riemann n’est toujours pas résolue. Elle affirme que les zéros non triviaux de la fonction zêta ont tous pour partie réelle 1/2… Ce qui nécessite dans doute quelques explications ! Lesquelles nous renverront à l’un des plus anciens thèmes des mathématiques : les nombres premiers.

Le problème de Monty Hall ou les probabilités changent de porte
Le paradoxe de Monty Hall dont le nom est tiré d’un jeu télévisé des années 60, concerne la façon dont l’information acquise en cours de jeu modifie (ou pas) les statistiques de gain. Résolu en théorie, la question perturbe tellement notre vision du monde qu’elle continue aujourd’hui encore d’être l’objet de débats passionnés.

Le paradoxe de Simpson ou les statistiques vues de biais
Les statistiques semblent, presque par nature, porter un discours positiviste. Elles sont en effet un formidable outil pour tenter de maîtriser la complexité du monde réel… Mais de nombreux « biais » menacent tout discours qui s’y réfère sans précautions : une lecture des chiffres trop simpliste peut nous amener - par exemple - à confondre corrélation et causalité… Et des phénomènes plus complexes (notamment le paradoxe de Simpson) peuvent fausser des conclusions qui semblent pourtant objectives.

Les géométries non-euclidiennes ou comment recréer le monde
Durant des siècles, la géométrie a reposé sur les postulats d’Euclide qui paraissaient éternels et irrévocables. Pourtant, l’un des postulats (le cinquième) a toujours semblé « un peu moins naturel » que les autres et des centaines de mathématiciens ont tenté en vain de s’en passer en le déduisant des autres postulats. Au milieu du XIXe siècle, Bernhard Riemann propose une idée neuve : imaginons qu’il est faux ! C’est l’acte de naissance des « géométries non- euclidiennes » qui connaitront un peu plus tard des applications majeures en physique.

Les pavages du plan ou les mathématiques du carrelage
Un pavage c’est une façon de couvrir un plan avec un motif répétitif… En gros, ça revient à créer un papier peint. En 1975, Marjorie Rice (1923- 2017), mère de famille et mathématicienne amateur, lit un article de Martin Gardner dans Scientific American qui liste TOUS les « pavages pentagonaux » possibles dans le plan. Un mathématicien vient justement de prouver que la liste était complète. Sauf que Marjorie, en travaillant toute seule chez elle, en trouve 4 nouveaux… Le théorème était faux !

La théorie des graphes ou comment éviter la grosse tête
La question est de savoir comment faire un réseau qui soit à la fois « économique » et « robuste » sans prendre trop de place. C’est une question théorique sur laquelle a travaillé le grand mathématicien russe Andrey Kolmogorov (1903-1987). Mais cette question théorique conditionne aussi la façon dont on peut construire un réseau informatique ou… un cerveau humain : pour être intelligent sans avoir la grosse tête, il faut un réseau de neurones qui soit efficace MAIS AUSSI compact !

Alicia Boole au pays des polytopes
On part des cinq « solides platoniciens » bien-aimés des géomètres : le cube, le tétraèdre, l’octaèdre, le dodécaèdre et l’icosaèdre. Platon les associait avec les éléments de base de la nature ; Kepler cherchait à les retrouver dans le mouvement des planètes... Mais pourquoi s’arrêter aux 3 dimensions de l’espace ordinaire ? Alicia Boole Stott a consacré sa vie à chercher des solides réguliers en dimension 4… et elle a trouvé ! Il existe un analogue 4-dimensionel de chacun des solides platoniciens. Et puis, il en existe aussi un sixième, l’ « icositétrachore », un animal spécifique à la quatrième dimension. Mentionner Ludwig Schlaflied, Alicia Boole, Charles Hinton…

La conjecture de Kepler ou comment ranger ses boulets
Formulée en 1611, la conjecture de Kepler concerne la meilleure façon d’empiler des oranges. Qui a dit que les mathématiques étaient trop abstraites ? La conjecture est prouvée par Thomas Hales en 1998… et avec une méthode qui ne plait pas beaucoup à ses collègues parce qu’il découpe le problème en une multitude de cas distincts qu’il traite par de méthodes informatiques. Dans la foulée de ce travail remis en cause par ses pairs, il s’intéresse à la certification des démonstrations mathématiques. En 2016, Maryna Viazovska (1984- ) démontre un « théorème d'empilement » équivalent en dimensions 8 et 24.
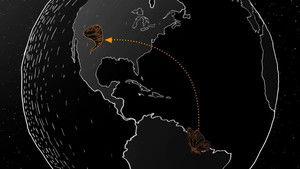
La théorie du chaos ou de l'ordre dans le désordre
"Le battement d'ailes d'un papillon au Brésil peut-il déclencher une tornade au Texas ?" Derrière le trop célèbre question posée par Edward Lorenz (1917-2008), il y a une théorie mathématique qui passe, dès sa conception par une image spectaculaire : celle des "attracteurs de Lorenz", et qui aboutit à une théorie de ce qui - jusque là - échappait au champ des mathématiques : les systèmes complexes, tels que ceux qui décrivent la météo ou encore... les affaires humaines !

La toupie de Kovalevskaïa ou la meilleure façon de tourner
En partant de questions astronomiques (problème des 3 corps, axe de rotation de la Terre...) on arrive aux notions de système stable et de dérivabilité en passant par le personnage de Sofia Kovaleskaya, mathématicienne qui a obtenu, à la fin du XIXe siècle, un résultat important concernant "le mouvement d'un solide autour d'un point fixe".

L'Entscheidungsproblem ou la fin des mathématiques ?
On entend souvent dire que les algorithmes contrôlent le monde. Mais qu'est-ce qu'un algorithme ? Pour les contemporains l'idée intuitive paraît à peu près clair : un algorithme, c'est ce qui peut "tourner sur un ordinateur". Mais c'est un renversement chronologique, puisque les ordinateurs concrets sont postérieurs, et viennent justement de travaux mathématique abstraits des années 1930. Nous les survolerons en compagnie de Alonzo Church, Jacques Herbrand, Kurt Gödel et Alan Turing.
Notes des Saisons
Casting Principal
Plateformes de Streaming pour Voyages au pays des maths
Bande-annonce
Questions Fréquemment Posées (FAQ) sur Voyages au pays des maths
Où puis-je regarder Voyages au pays des maths en streaming ?
Vous pouvez regarder Voyages au pays des maths sur différentes plateformes de streaming en France : Vérifiez la disponibilité sur les principales plateformes de streaming françaises comme Netflix, Amazon Prime Video, Disney+ et d'autres services légaux.
Est-ce que Voyages au pays des maths est disponible en français (doublé/sous-titré) ?
Oui, Voyages au pays des maths est disponible avec audio et sous-titres en français sur la plupart des plateformes de streaming. Veuillez vérifier la disponibilité du doublage français sur votre plateforme préférée.
Quel est le synopsis de Voyages au pays des maths ?
C’est un pays exotique et déroutant que celui des maths. On y parle une langue bizarre, pleine d’homéomorphismes, de variétés différentielles, de nombres transfinis… Mais on y trouve aussi des paysages épiques, des idées vertigineuses et même, parfois, des choses utiles ! Cette websérie animée propose à tous les curieux munis d’un cerveau en état de marche une visite inédite au pays des maths. Avec un guide, bien sûr !
Qui sont les acteurs principaux de Voyages au pays des maths ?
Le casting principal de Voyages au pays des maths comprend : Informations sur le casting non disponibles pour le moment.
Quelle est la note de Voyages au pays des maths ?
Voyages au pays des maths a reçu une note de 8.5/10 basée sur 2 votes d'utilisateurs.
Explorez du contenu similaire :
Avis et Commentaires sur Voyages au pays des maths
Aucun commentaire public n'a encore été posté sur ce série TV. Soyez le premier à partager votre avis !
Ajouter un Commentaire
Connectez-vous ou créez un compte pour ajouter un commentaire.





💬 Avez-vous vu Voyages au pays des maths ?
Partagez votre avis ! Les avis des utilisateurs nous aident à créer la meilleure communauté de passionnés de films et séries TV en France.
Inscrivez-vous maintenant pour laisser votre avis et aider d'autres utilisateurs à découvrir de nouveaux contenus à regarder !